« poprzedni punkt   następny punkt »


2. Iloczyn wektorowy

W tym punkcie wykładu zajmiemy się badaniem prostych zależności między obiektami geometrycznymi jakimi są punkt, prosta i  wektor. Dobór problemów nie jest przypadkowy:  poruszymy te problemy elementarne, które pojawią się w następnych punktach, gdzie będzie mowa o jednym z centralnym problemów geometrii obliczeniowej, jakim jest problem otoczki wypukłej. Okazuje się, że większość z nich można rozwiązać za pomocą operacji produktu wektorowego i/lub wykorzystując jego właściwości. Stąd tytuł tego punktu.
 

Niech p1 i p2 będą dwoma punktami na płaszczyźnie, p1 = (p1.x, p1.y), p2 = (p2.x, p2.y). Iloczynem wektorowym wektorów zaczepionych w początku układu współrzędnych i o końcach odpowiednio w punktach p1 i p2 jest wektor x =  p1 ´ p2  prostopadły do obu wektorów, taki że trójka uporządkowana p1, p2 , x ma orientację dodatnią oraz długość wektora x,  |x| = |p1| *|p2| * sin j gdzie j jest kątem między tymi wektorami.

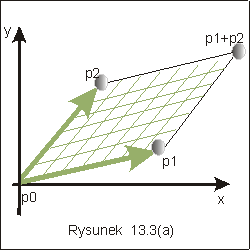
Dla celów tego wykładu, najważniejsza okazuje się interpretacja wartości  | p1 x p2|, jako pola równoległoboku, utworzonego przez punkty (0,0), p1, p2, i p1+ p2, opatrzonego znakiem, por. rysunek 13. 3(a), oraz  fakt, że wartość tego pola można wyliczyć jako wartość wyznacznika utworzonego przez współrzędne wektorów  p1 i p2.

| p1 ´ p2| =  det( p1 , p2 ) = p1.x  * p2.y - p2.x  *p1.y.

Na podstawie tego ostatniego wzoru, jest oczywiste, że  |p2 ´ p1| = -|p1 ´ p2|. Wynika stąd jeszcze, że znak wyznacznika det( p1, p2 ) mówi o wzajemnym położeniu wektorów p1, p2.
Rozważmy jeszcze nieco ogólniejszą sytuację:  niech będą dwa odcinki p0p1  i p0p2  zaczepione w punkcie p0 i skierowane w stronę p1 i p2 odpowiednio. Aby stwierdzić jak są one położone względem siebie, przesuniemy punkt wspólny p0 do początku układu współrzędnych.  W wyniku przesunięcia otrzymamy wektory (p1-p0 ) i (p2-p0), których wzajemne położenie jest takie samo, jak wektorów  p0p1  i p0p2 .

Lemat 2.1 Niech   p0, p1, p2 będą dowolnymi punktami na płaszczyźnie i niech D będzie wartością   | (p1-p0) x (p2-p0)| .

Z lematu 2.1 wynika, że  jeśli  | (p1-p0) ´ (p2-p0)| >0, to p2 jest położone względem p1 przeciwnie do ruchu wskazówek zegara,  lub inaczej, przesuwając się wzdłuż wektora od  punktu p0 do p1, punkt p2 mamy zawsze po lewej ręce, por. rysunek 13.3(b). Natomiast na rysunku 13.3(c) punkt  p2 leży w kierunku zgodnym z ruchem wskazówek zegara względem p1.

Przykład 2.1
Rozważmy  punkty p 0 = (1,0), p1 = (0,1) oraz p2 =(1,1). Punkt p2 leży na  prawo od wektora p0p1. Rzeczywiście det( p1-p0, p2-p0) = 1*(-1) - 1*0 < 0.
Natomiast punkt q2 = (1/4,1/4) leży na lewo od wektora p1-p0.

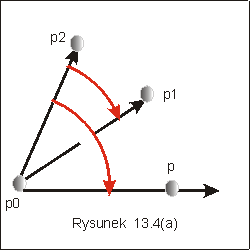
Problem I  Jak porównać dwa kąty nie licząc ich wartości?  Niech sytuacja będzie taka jak przedstawiono na rysunku 13.4a.  Który z kątów  (p1,p0,p), czy (p2,p0,p) jest większy?  Wystarczy stwierdzić jakie jest wzajemne położenie  wektorów  p0p1 i p0p2. Liczymy w tym celu wyznacznik  det (p1- p0, p2 - p00). Jeżeli jego znak jest dodatni, to kąt(p2 p0 p) jest większy niż  kąt( p1p0p).

porownanie katów
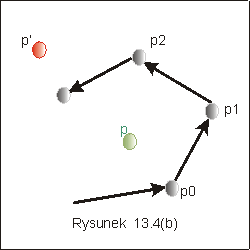 punt wzgl wielokąta


Problem II Niech będą dane punkty tworzące wielokąt wypukły, por. rysunek 13.3c. Jak sprawdzić, czy dany punkt jest, czy nie jest we wnętrzu tego wielokąta? Wystarczy w tym celu sprawdzić, czy dany punkt jeży na lewo od prostych będących przedłużeniem boków wielokąta idąc wzdłuż krawędzi w kierunku od p0 do p3. Punkt p na rysunku 13.4(b) spełnia ten warunek, a punkt p' nie spełnia. Wprawdzie leży na lewo od wektorów p0p1, p1p2, p2p3, ale jest na prawo od prostej wyznaczonej przez krawędź p2p3.

Zauważmy, że sprawdzenie, po której stronie prostej leży dany punkt ma koszt stały, ale w przypadku problemu sprawdzenia czy dany punkt leży wewnątrz wielokąta wypukłego, wymaga wykonania liczby kroków równej liczbie krawędzi wielokąta.

Pytanie 2: Rozważmy trzy punkty na płaszczyźnie (0,1), (1,0), (3,3). Czy punkt (2,2.5) leży wewnątrz, czy na zewnątrz trójkąta utworzonego przez te punkty?


« poprzedni punkt   następny punkt »