1. Algorytmy cyrkla i linijki

Do wielu zasług Euklidesa możemy dodać jeszcze tę, że wprowadził w geometrii pojęcie konstrukcji euklidesowej, tzn. metody, w której opisano zestaw środków z jakich wolno nam korzystać, zestaw elementarnych akcji jakimi możemy się posługiwać, oraz metodę postępowania prowadzącą do powstania obiektu geometrycznego. Konstrukcja euklidesowa, to nic innego jak algorytm działający w specyficznym środowisku.
Algorytmy omawiane w tym punkcie, to konstrukcje euklidesowe, wykorzystujące operacje, których nauczyliśmy się w szkole podstawowej, a wykonujemy je na papierze za pomocą cyrkla i linijki.

Problem Obliczanie pierwiastka kwadratowego z liczby całkowitej.
Niech odcinek xy reprezentuje jedność. Zadanie polega na znalezieniu pierwiastka kwadratowego z danej liczby naturalnej n, sqrt(n).

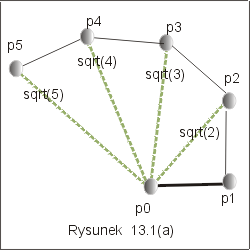
Najprostsze rozwiązanie wykorzystuje twierdzenie Pitagorasa. Jeśli jeden z boków trójkąta prostokątnego reprezentuje liczbę sqrt(i), a drugi liczbę 1, to przeciwprostokątna odpowiada liczbie sqrt(i+1) por. rysunek 13.1(a).

Algorytm 1

SQRT1	(n : int){
	Narysuj odcinek jednostkowy o początku w punkcie x i końcu w punkcie y.
	p[0]:= x; p[1] := y;
	i := 1;
	while (i < n) do
	Wystaw prostą prostopadłą do odcinka x, p[i] w punkcie p[i].
	Zaznacz na niej punkt p[i+1] w odległości 1 od punktu p[i].
	i := i+1;
	od
}

Niezmiennikiem pętli w tym algorytmie jest własność:

Odcinek xp[i] reprezentuje liczbę sqrt(i).

Rzeczywiście, dla i=1 własność jest spełniona, bo z założenia odcinek xy reprezentuje jedność. Jeśli w i-tym kroku długość odcinka xp[i] wynosi sqrt(i), i zbudujemy trójkąt prostokątny o jednym boku równym xp[i], a drugim równym jedności, to przekątna na mocy twierdzenia Pitagorasa ma długość sqrt(i+1). Po wykonaniu n-1 kroków, wychodzimy z pętli z i = n oraz odcinkiem xp[n] długości sqrt(n).

Wszystkie operacje tego algorytmu można zrealizować za pomocą cyrkla i linijki.

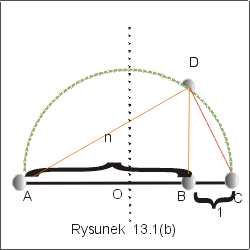
Inne rozwiązanie tego samego problemu polega na wykorzystaniu twierdzenia Pitagorasa i własności, że kąt oparty na średnicy koła jest prosty, por. rysunek 13.1(b).

Algorytm 2

SQRT2	(n : int){
	Narysuj linię prostą L i zaznacz na niej punkt początkowy A.
	p[0]:= A;
	for i:=1 to n+1 do
	Zaznacz na prostej L punkt p[i] odległy od p[i-1] o jednostkę
	od;
	Niech C=p[n+1].
	Znajdź środek odcinka AC. Niech to będzie punkt O.
	Z punktu O narysuj okrąg o promieniu równym połowie odcinka AC.
	W punkcie B=p[n] wystaw prostą prostopadłą do prostej L;
	Zaznacz punkt D, przecięcia okręgu i tej prostej.
}

Poprawność

Z konstrukcji wynika, że BC będzie odcinkiem jdnostkowym, a AC zawiera (n+1) jednostek. Ponieważ trójkąty ADC, ADB i DBC są trójkątami prostokątnymi, zatem

n² +DB² = AD², 1+DB² = DC² , (n+1)² = AD² +DC².

Stąd (n+1)²= n² +1 + 2 DB² i ostatecznie sqrt(n) = DB.

Problem II Dany odcinek AB podzielić go na n równych części.

W tym przypadku zastosujemy twierdzenie Talesa, por. rysunek 13.2(a).

Algorytm 3

Podziel	(n : int){
	Z punktu A odcinka AB narysuj dowolną prostą. Ustal odcinekjednostkowy.
	p[0]:= A;
	for i:=1 to n do
	Zaznacz na prostej L punkt p[i] odległy od p[i-1] o jednostkę
	od;
	Niech C=p[n].
	Poprowadź prostą przez punkty C, B i niech B = q[n];
	for i := n-1 downto 1 do
	Wystaw prostą równoległą do prostej BC i przechodzącą przez punkt p[i]
	Zaznacz punkt przecięcia tej prostej z L, q[i]
	od}

Punkty q[i] dzielą odcinek AB na n równych części. Rysowanie prostej równoległej do danej prostej i przechodzącej przez dany punkt nie jest całkiem proste, ale całkowicie da się wykonać za pomocą cyrkla i linijki. A oto algorytm, por. rysunek 13.2(b):

1. Niech X=p[i]. Z punktu X zakreśl okrąg promieniem o długości 1.
2. Punkt przecięcia z prostą BC oznaczmy przez D. Powstał trójkąt równoramienny o wierzchołkach X,C,D.
3. Podziel odcinek DC (podstawa trójkąta) na połowę i znajdź punkt środkowy Y. Odcinek XY jest wysokością trójkąta i równocześnie odległością szukanej prostej równoległej od prostej BC.
4. Z punktu B zaznacz punkt q[i], odległy od B o długość odcinka XY. Wyznaczony właśnie odcinek to 1/m danego odcinka AB.

Pytanie 1: Jak podzielić dany kąt ABC na połowę? Zaproponuj algorytm.

« poprzedni punkt następny punkt »