W tym punkcie wrócimy na chwilę do znanych nam już algorytmów przeglądania grafu metodą "wszerz" BFS i "w głąb" DFS, por. wykład VII p1 . Wykorzystamy, je najpierw do zbadania, czy dany graf niezorientowany jest spójny, a następnie do budowy drzewa rozpinającego grafu.

Idea przeglądania grafu metodą BFS "wszerz" polega na przeszukaniu najpierw węzłów odległych o jedną krawędz od wybranego wierzchołka, następnie o dwie krawędzie od wybranego wierzchołka itd. Algorytm wykorzystuje kolejkę FIFO do przechowywania wierzchołków, których następniki nie zostały jeszcze odwiedzone. Musimy dodatkowo zadbać by nie wpisywać do kolejki wierzchołków, które już wcześniej tam wpisaliśmy. Dla każdego węzła grafu będziemy więc pamiętali, czy został on już "odwiedzony" lub "zamarkowany", co tutaj oznacza "wpisany do kolejki", czy nie. Można to zrealizować w zwykłej tablicy boolowskiej m, gdzie m[i] = true oznacza, że wierzchołek i-ty był już odwiedzony w trakcie dotychczasowego przeglądania grafu.

Szkic algorytmu BFS

1.Włóż do kolejki q wybrany wierzchołek grafu i zamarkuj go.
2. Dopóki kolejka q nie jest pusta :
            Wez pierwszy element kolejki q.
            Dopisz do kolejki wszystkie wierzchołki z nim incydentne, o ile nie były jeszcze zamarkowane i
            każdy z nich zamarkuj.
            Usuń pierwszy element kolejki q.

Idea przeglądania grafu metodą DFS "w głąb" polega na rekurencyjnym odwiedzaniu wierzchołków coraz bardziej odległych od wierzchołka początkowego, wzdłuż jednej ścieżki, tak daleko jak to jest możliwe. Jeśli kontynuacja nie jest możliwa, wracamy do poprzedniego wierzchołka, wybieramy jakiś nieodwiedzony wierzchołek z jego listy incydencji i powtarzamy postępowanie.

1.Zaznacz wybrany wierzchołek jako odwiedzony.
2. Dla każdego wierzchołka z listy incydencji wybranego wierzchołka:
Jeśli wierzchołek nie był jeszcze zamarkowany, to
zastosuj rekurencyjnie procedurę odwiedzania do tego wierzchołka.

Rozważmy graf z rysunku 12.2. Zakładając, że numeracja wierzchołków odpowiada porządkowi alfabetycznemu ich nazw, oraz że zaczynamy przeglądanie wierzchołków grafu od wierzchołka A, a porządek na listach incydencji jest porządkiem alfabetycznym, to kolejność odwiedzania metodą BFS będzie następująca: A, B, F, G, C, E, I, H, D. Natomiast kolejność odwiedzania metodą DFS : A, B, C, D, E, F, I, G, H.

Koszt
Koszt postępowania w obu algorytmach jest podobny. Dla każdego wierzchołka grafu przeglądamy jego listę incydencji. W przypadku BFS, każdy wierzchołek może być co najwyżej raz wpisany do kolejki, bo po wpisaniu markujemy go jako odwiedzony. W przypadku metody "w głąb", procedurę DFS wywołuje się rekurencyjnie co najwyżej raz dla każdego wierzchołka, gdyż wywołuje się ją tylko dla wierzchołków niezamarkowanych, a każde wywołanie DFS powoduje zamarkowanie wierzchołka będącego argumentem procedury. Pętle w obu algorytmach są zatem skończone. Ponieważ, w najgorszym razie, przeglądamy wszystkie krawędzie grafu., zatem koszt przeglądania można w obu przypadkach oszacować przez O(|V| + |E|), gdzie V jest zbiorem wierzchołków, a E zbiorem krawędzi grafu.

Zwróćmy uwgę, że postępownie opisane w metodach BFS i DFS nie musi koniecznie spowodować odwiedzenia wszystkich wierzchołków grafu. Jeżeli w danym grafie są wierzchołki, nie połączone żadną drogą, to zaczynając odwiedzanie grafu od jednego z nich, nigdy nie dojdziemy do drugiego. Odwrotnie, jeżeli przechodzenie grafu metodą BFS lub DFS nie spowoduje odwiedzenia wszystkich wierzchołków grafu, to tylko dlatego, że między jakimiś wierzchołkami grafu nie istnieje droga, tzn. są takie wierzchołki, że jeden z nich nie jest osiągalny z drugiego. Wynika stąd, że algorytmy BFSi DFS można użytć do badania spójności grafu: jeśli po zakończeniu algorytmu wszystkie wierzchołki były odwiedzone, to graf jest spójny, jeśli istnieją jeszcze nieodwiedzone wierzchołki, to graf nie jest spójny.

Niech G będzie grafem, którego wierzchołki zostały ponumerowane liczbami natualnymi, od 1 do n. Przyjmijmy, że graf jest przedstawiony w postaci tablicy list incydencji Tab. Tab[i] jest listą incydencji wierzchołka itego. Załóżmy, że lista incydencji jest zbudowana z obiektów, których atrybutami są val- numer wierzchołka i next- referencja do następnego obiektu listy. Dodatkowo, niech m będzie tablicą, w której zaznaczymy, które wierzchołki zostały już odwiedzone.

Algorytm DFS - Badanie spójności grafu

Załóżmy teraz, że graf G jest spójny i zmodyfikujmy algorytmy przeglądania w taki sposób, by wypisywały krawędzie, którymi dochodzi się do kolejno odwiedzanych wierzchołków. Zbiór odwiedzonych krawędzi tworzy drzewo, gdyż nie ma w nim cykli: funkcje BFS i DFS powodują odwiedzanie tylko nie odwiedzonych jeszcze wierzchołków. Drzewa uzyskane w ten sposób, nazywamy drzewami przeszukiwania "wszerz" i "w głąb" odpowiednio. Ponieważ, w przypadku, gdy graf jest spójny, zostaną odwiedzone wszystkie wierzchołki grafu, zatem drzewa przeszukiwań są drzewami rozpinającymi grafu. Algorytmy przeglądania DFS i BFS można więc wykorzystać do konstruowania drzewa rozpinającego grafu.

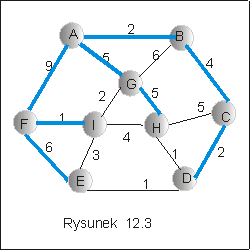
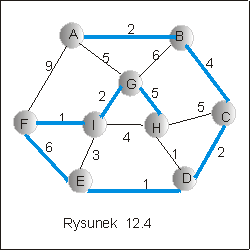
Przykład 2.2
Na rysunku 12.3 przedstawiono wynik działania procedury BFS_ST, a na rysunku 12.4 wynik działania procedury DFS_ST: dwa drzewa rozpinające grafu z rysunku 12.2 .

Pytanie 3: Jaki jest koszt drzewa rozpinającego niezorientowanego grafu spójnego o n wierzchołkach i m krawędziach, jeśli funkcja kosztu tego grafu przyjmuje stale wartość const?

DFS	(v : integer){
	m[v] := true; x := Tab[v];
	while (not x = null) do	//przeglądamy listę incydencji węzła v
	w := x.val;
	if (m[w] = false) then DFS(w) fi	// o ile w nie był odwiedzony
	x := x.next;	//wywołujemy rekurencyjnie DFS
	od;
	result := true;	// badamy, czy wszystkie wierzchołki
	for i := 1 to n do result :=m[i] and result; od;	//były zamarkowane
}

BFS	(v : integer){
	q := in(v,q) ;
	while (not empty(q)) do
	v := first(q); q := out(q);
	x := Tab[v];
	while (not x= null) do	//przeglądamy listę incydencji węzła v
	w := x.val;
	if (m[w] = false) then	// o ile w nie był odwiedzony
	q := in(w,q); m[w]:= true	//wpisujemy go do kolejki i markujemy
	fi;
	x := x.next;
	od;
	od;
	result := true;	// badamy, czy wszystkie wierzchołki
	for i := 1 to n do result :=m[i] and result; od;	//były zamarkowane
}

DFS_ST	(v : integer){
	m[v] := true; x := Tab[v];	//Niezmiennik pętli:
	while (not x = null) do	//Zbiór wypisanych krawędzi tworzy drzewo
	w := x.val;
	if (m[w] = false) then
	m[w] := true;
	wypisz krawędź (v,w);
	DFS(w);
	fi;
	x := x.next;
	od;
}

BFS_ST	(v : integer){
	q := in(v,q) ;
	while (not empty(q)) do	// Niezmiennik:
	v := first(q); q := out(q);	// zbiór wypisanych krawędzi tworzy drzewo
	x := Tab[v];
	while (not x= null) do
	w := x.val;
	if (m[w] = false) then fi
	q := in(w,q); m[w]:= true
	wypisz krawędź (v,w);
	fi;
	x := x.next;
	od;
	od;
}