


| « poprzedni punkt | następny punkt » |
Niech G = <V, E> będzie dowolnym grafem niezorienowanym, spójnym.
Przykład 1.1
Na rysunku 12.1 przedstawiono graf niezorientowany i trzy różne drzewa
rozpinające tego grafu.
 |
 |
 |
Uwaga. Drzewo rozpinające grafu o n wierzchołkach ma n
wierzchołków
i n-1 krawędzi.
Przyklad 1.2
Uwaga
Używamy tu słowa "koszt" dla funkcji przypisującej wartości
krawędziom, jednak interpretacją dla wartości tej funkcji może być
odległość, czas, ciężar, czy dowolny inny parametr charakteryzujący
krawędz, zależnie od konkretnej sytuacji i zastosowania, w którym
rzeczywistą sytuację modelujemy jako graf. W literaturze używa się
nazwy "wagi krawędzi", jednak w tym kursie słowo "waga" zostało
zarezerwowane dla wag wierzchołów w drzewach AVL.
Przykład 1.3
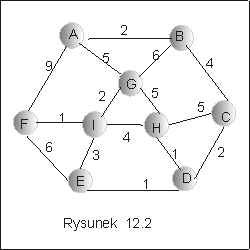 |
Pytanie 1: A jaki jest
koszt
minimalnego drzewa rozpinającego grafu 12.2?
Zastanówmy się przez chwilę, jakie
założenia muszą być spełnione, by istniało minimalne drzewo rozpinające
grafu niezorientowanego. Jest oczywiste, że graf,
który nie jest spójny nie ma drzewa rozpinającego: istnieją w tym
grafie co najmniej dwa wierzchołki, których nie można połączyć
żadną drogą. Dlatego też pojęcie drzewa rozpinającego definiujemy
dla grafów niezorientowanych spójnych.
Łatwo zauważyć, że graf, który ma drzewo rozpinające, może mieć więcej
niż jedno minimalne drzewo rozpinające. Trywialnym przykładem jest
graf, w którym funkcja kosztu jest stała: wszystkie krawędzie mają
przypisaną tę samą wartość. Wtedy oczywiście jest wiele różnych
drzew
rozpinających. A kiedy minimalne drzewo rozpinające jest
wyznaczone jednoznacznie? Odpowiedzią na to pytanie jest następujący
lemat.
Dowód.
Niech G będzie grafem spójnym o n
wierzchołkach i przypuśćmy, ze istnieją dwa drzewa rozpinające
grafu G o minimalnym koszcie, T1 i T2. Niech
będą odpowiednio ciągami wszystkich krawędzi drzew T1 i T2, uporządkowanymi rosnąco ze względu na funkcję kosztu. Przyjmijmy, że i jest największym indeksem, takim że krawędzie drzew o mniejszych indeksach są identyczne, tzn. e'1= e"1, e'2= e"2, ..., e'i-1= e"i-1. Ponieważ funkcja kosztu jest w tym grafie różnowartościowa (z założenia) oraz krawędzie na pozycji i-tej są różne, to c(e'i ) różni się od c(e"i ). Niech c(e'i ) < c(e"i ), dla ustalenia uwagi. Ponieważ krawędz e'i nie należy do T2, więc dołączenie jej do T2 spowoduje powstanie cyklu. Gdyby wszystkie krawędzie tego cyklu należały do T1, to w T1 też byłby cykl. Ponieważ tak nie jest (T1 jest drzewem), więc istnieje krawędz e w tym cyklu, która nie należy do T1. Wynika stąd, że krawędz e musi, w uporządkowanym ciągu wszystkich krawędzi, znajdować się na pozycji większej niż i, czyli c(e'i ) < c(e). Rozważmy teraz graf T3, który powstaje z T2 przez odrzucenie krawędzi e i dołączenie krawędzi e'i . T3 jest acyklicznym grafem, ma n wierzchołków i n-1 krawędzi. Jest to więc drzewo rozpinające grafu G, ale
Doszliśmy do sprzeczności z
założeniem, e T2 jest minimalnym drzewem rozpinającym, co dowodzi, że
w rozważanym przypadku istnieje dokładnie jedno minimalne drzewo
rozpinające grafu.
Na zakończenie tego punktu zwróćmy uwagę, że minimalne drzewo
rozpinające grafu nie musi być drzewem najkrótszych ścieżek z pewnego
ustalonego wierzchołka. Na rysunku 12.2(a) przedstawiono drzewo
najkrótszych ścieżek z wierzchołka A. Jest to oczywiście drzewo
rozpinające grafu. Nie jest jednak minimalne. Minimalne drzewo
rozpinające tego grafu przedstawiono na rysunku 12.2(b). Oczywiście,
mamy tu ścieżki z A do każdego wierzchołka, ale niekoniecznie
najkrótsze.
 |
 |
Pytanie 2: Jeżeli D jest drzewem
rozpinającym pewnego acyklicznego i spójnego grafu niezorientowanego o
m krawędziach, to ile wierzchołków ma to drzewo?
| « poprzedni punkt | następny punkt » |