| Nr | Opcja | Punkty | Poprawna | Odpowiedź |
|---|
| 1 | Rozważmy funkcje zmiennej 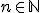 . Które z poniższych zdań jest prawdziwe? . Które z poniższych zdań jest prawdziwe? |
| 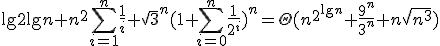 | 0 | | |
| 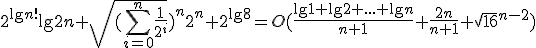 | 0 | | |
| Ciąg funkcji  jest ciągiem ściśle malejącym względem ich rzędów jest ciągiem ściśle malejącym względem ich rzędów | 1 | + | |
| 2 | Rozważmy drzewo 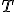 typu AVL powstałe na skutek kolejnego wstawiania elementów ciągu typu AVL powstałe na skutek kolejnego wstawiania elementów ciągu 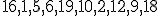 do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe? do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe? |
| Wysokość drzewa 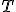 jest równa dokładnie jest równa dokładnie 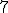 | 0 | | |
| Łączna liczba rotacji pojedynczych w lewo wykonanych w trakcie budowy drzewa 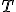 jest równa dokładnie jest równa dokładnie 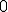 | 1 | + | |
| Liczba wierzchołków wewnętrznych drzewa 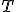 jest równa dokładnie jest równa dokładnie 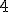 | 0 | | |
| 3 | Rozważmy nieskierowany graf prosty 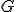 , którego wierzchołki etykietowane są liczbami naturalnymi od , którego wierzchołki etykietowane są liczbami naturalnymi od 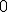 do do 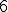 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 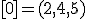 , , 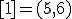 , , 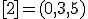 , , 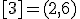 , , 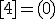 , , 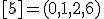 , , 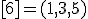 i przedstawiony na poniższym rysunku. Wierzchołki grafu i przedstawiony na poniższym rysunku. Wierzchołki grafu 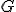 odwiedzamy w kolejności BFS z wierzchołka startowego odwiedzamy w kolejności BFS z wierzchołka startowego 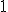 .
Które z poniższych zdań jest prawdziwe? Uwaga! W algorytmie BFS
wierzchołki grafu umieszczamy w kolejce pomocniczej w kolejności
rosnących wartości etykiet. .
Które z poniższych zdań jest prawdziwe? Uwaga! W algorytmie BFS
wierzchołki grafu umieszczamy w kolejce pomocniczej w kolejności
rosnących wartości etykiet. 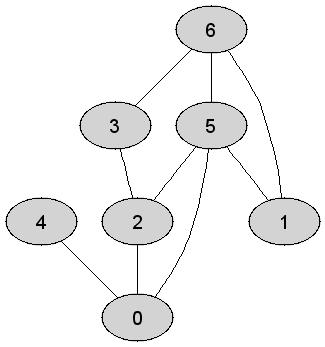
|
| Kolejność odwiedzenia wierzchołków jest następująca: 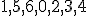 | 1 | + | |
| Liczba operacji OUT w kolejce pomocniczej w trakcie wykonania algorytmu BFS jest równa dokładnie 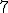 | 1 | + | |
| Maksymalna długość kolejki pomocniczej w trakcie wykonania algorytmu BFS jest równa dokładnie 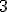 | 1 | + | |
| 4 | Rozważmy drzewo 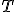 typu BST powstałe na skutek kolejnego wstawiania elementów ciągu typu BST powstałe na skutek kolejnego wstawiania elementów ciągu 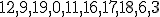 do początkowo pustej struktury (przy użyciu operacji INSERT). Następnie z drzewa do początkowo pustej struktury (przy użyciu operacji INSERT). Następnie z drzewa 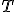 usuwamy wierzchołki z etykietami usuwamy wierzchołki z etykietami 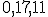 .
Które z poniższych zdań jest prawdziwe?. Uwaga! W razie konieczności w
operacji DELETE w miejsce usuwanego wierzchołka wstawiamy wierzchołek
bezpośrednio poprzedni (drzewo .
Które z poniższych zdań jest prawdziwe?. Uwaga! W razie konieczności w
operacji DELETE w miejsce usuwanego wierzchołka wstawiamy wierzchołek
bezpośrednio poprzedni (drzewo 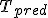 ) albo następny (drzewo ) albo następny (drzewo 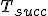 ) względem porządku etykiet. ) względem porządku etykiet. |
| Wysokość drzewa 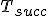 jest równa dokładnie jest równa dokładnie 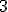 | 1 | + | |
| Liczba wierzchołków zewnętrznych drzewa 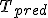 jest równa dokładnie jest równa dokładnie 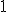 | 0 | | |
| Etykiety wierzchołków drzewa 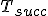 wypisane w kolejności PostOrder tworzą ciąg: wypisane w kolejności PostOrder tworzą ciąg: 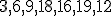 | 1 | + | |
| 5 | Rozważmy pełne drzewo binarne 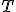 wysokości wysokości 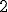 . Które z poniższych zdań jest prawdziwe? . Które z poniższych zdań jest prawdziwe? |
| Jeżeli wierzchołki drzewa 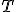 w kolejności InOrder tworzą ciąg w kolejności InOrder tworzą ciąg 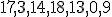 , to w kolejności PreOrder tworzą ciąg: , to w kolejności PreOrder tworzą ciąg: 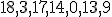 | 1 | + | |
| Jeżeli wierzchołki drzewa 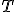 w kolejności PreOrder tworzą ciąg w kolejności PreOrder tworzą ciąg 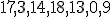 , to w kolejności InOrder tworzą ciąg: , to w kolejności InOrder tworzą ciąg: 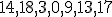 | 0 | | |
| Jeżeli wierzchołki drzewa 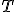 w kolejności PostOrder tworzą ciąg w kolejności PostOrder tworzą ciąg 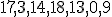 , to w kolejności InOrder tworzą ciąg: , to w kolejności InOrder tworzą ciąg: 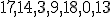 | 1 | + | |
| 6 | Rozważmy nieskierowany graf prosty 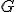 , którego wierzchołki etykietowane są liczbami naturalnymi od , którego wierzchołki etykietowane są liczbami naturalnymi od 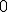 do do 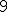 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 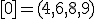 , , 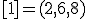 , , 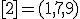 , , 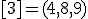 , , 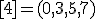 , , 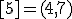 , , 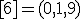 , , 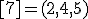 , , 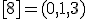 , , 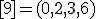 i przedstawiony na poniższym rysunku. Dla grafu i przedstawiony na poniższym rysunku. Dla grafu 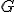 stosujemy algorytm kolorowania LF (largest first). Które z poniższych
zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości
wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą
etykietą. Kolory indeksujemy od
stosujemy algorytm kolorowania LF (largest first). Które z poniższych
zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości
wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą
etykietą. Kolory indeksujemy od 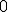 . . 
|
| Liczba chromatyczna 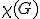 grafu grafu 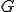 jest równa dokładnie jest równa dokładnie 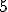 | 0 | | |
| Liczba chromatyczna 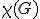 grafu grafu 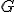 jest równa dokładnie jest równa dokładnie 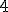 | 0 | | |
| Po zastosowaniu algorytm LF wierzchołek 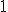 ma przypisany taki sam kolor jak wierzchołek ma przypisany taki sam kolor jak wierzchołek 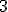 | 1 | + | |
| 7 | Rozważmy
wykonanie algorytmu obliczania wartości poprawnie i w pełni
nawiasowanego wyrażenia arytmetycznego, przy użyciu dwóch stosów: stosu
argumentów i stosu operatorów. Wyrażenie wejściowe ma postać 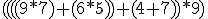 . Które z poniższych zdań jest prawdziwe? . Które z poniższych zdań jest prawdziwe? |
| Liczba operacji POP na stosie argumentów w trakcie wykonania algorytmu jest równa dokładnie 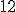 | 1 | + | |
| Liczba operacji PUSH na stosie argumentów w trakcie wykonania algorytmu jest równa dokładnie 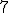 | 0 | | |
| Liczba operacji POP na stosie argumentów w trakcie wykonania algorytmu jest równa dokładnie 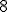 | 0 | | |
| 8 | Rozważmy kopiec binarny 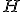 typu min zaimplementowany w drzewie binarnym. Kopiec typu min zaimplementowany w drzewie binarnym. Kopiec 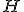 konstruujemy z elementów ciągu konstruujemy z elementów ciągu 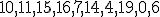 stosując szybki algorytm budowy kopca HeapConstruct. Które z poniższych zdań jest prawdziwe? stosując szybki algorytm budowy kopca HeapConstruct. Które z poniższych zdań jest prawdziwe? |
| Wysokość drzewa-kopca 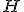 jest równa dokładnie jest równa dokładnie 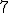 | 0 | | |
| Liczba operacji przestawień elementów kopca wykonanych w trakcie jego budowy jest równa co najwyżej 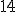 | 1 | + | |
| Etykiety wierzchołków drzewa-kopca 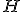 wypisane w kolejności PostOrder tworzą ciąg: wypisane w kolejności PostOrder tworzą ciąg: 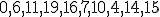 | 0 | | |
| 9 | Rozważmy drzewo kodowe Huffmana 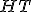 powstałe na skutek zastosowania algorytmu budowy drzewa kodu Huffmana
dla ciągu znaków zawierającego odpowiednio (znak - krotność wystąpień):
powstałe na skutek zastosowania algorytmu budowy drzewa kodu Huffmana
dla ciągu znaków zawierającego odpowiednio (znak - krotność wystąpień):
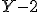 , , 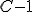 , , 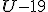 , , 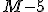 , , 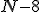 , , 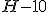 , , 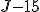 , , 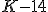 .
Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku
niejednoznacznego wyboru poddrzew, za mniejsze uznajemy to, którego
etykiet liści czytane od lewej do prawej strony tworzą słowo mniejsze w
sensie porządku leksykograficznego. .
Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku
niejednoznacznego wyboru poddrzew, za mniejsze uznajemy to, którego
etykiet liści czytane od lewej do prawej strony tworzą słowo mniejsze w
sensie porządku leksykograficznego. |
| Wysokość drzewa 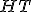 jest równa dokładnie jest równa dokładnie 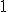 | 0 | | |
| Wysokość drzewa 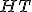 jest równa dokładnie jest równa dokładnie 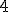 | 0 | | |
| Kod litery 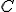 odczytany z drzewa odczytany z drzewa 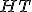 jest następujący: jest następujący: 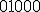 | 1 | + | |
| 10 | Rozważmy tablicę 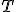 reprezentującą reprezentującą 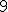 -elementowy ciąg różnych liczb naturalnych: -elementowy ciąg różnych liczb naturalnych: 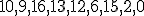 . W owej tablicy wyszukujemy indeksu elementu . W owej tablicy wyszukujemy indeksu elementu 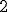 -go
co do wielkości za pomocą algorytmu Hoare'a z procedurą podziału zgodną
z metodą Partition. Które z poniższych zdań jest prawdziwe? -go
co do wielkości za pomocą algorytmu Hoare'a z procedurą podziału zgodną
z metodą Partition. Które z poniższych zdań jest prawdziwe? |
| W rozważanym przypadku liczba wykonanań algorytmu Partition jest równa dokładnie 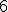 | 1 | + | |
| W
rozważanym przypadku liczba wykonanań algorytmu Partition jest większa
od liczby wykonań tego algorytmu, gdy zamiast indeksu elementu 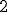 -go co do wielkości będziemy wyszukiwali indeksu elementu -go co do wielkości będziemy wyszukiwali indeksu elementu 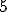 -go co do wielkości -go co do wielkości | 1 | + | |
| Argumentem 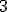 -go wykonania algorytmu Partition jest tablica postaci: -go wykonania algorytmu Partition jest tablica postaci: 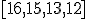 , w której szukamy indeksu elementu , w której szukamy indeksu elementu 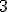 -go co do wielkości -go co do wielkości | 0 | | |
| 11 | Rozważmy nieskierowany graf prosty 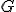 z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od 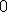 do do 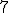 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 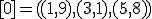 , , 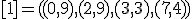 , , 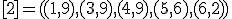 , , 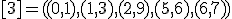 , , 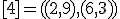 , , 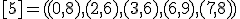 , , 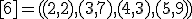 , , 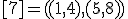 i przedstawiony na poniższym rysunku. Dla grafu i przedstawiony na poniższym rysunku. Dla grafu 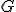 stosujemy algorytm Kruskala wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru krawędzi, jako pierwszą
wybieramy krawędź, której etykiety wierzchołków krańcowych w kolejności
niemalejącej tworzą mniejszą liczbę naturalną.
stosujemy algorytm Kruskala wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru krawędzi, jako pierwszą
wybieramy krawędź, której etykiety wierzchołków krańcowych w kolejności
niemalejącej tworzą mniejszą liczbę naturalną. 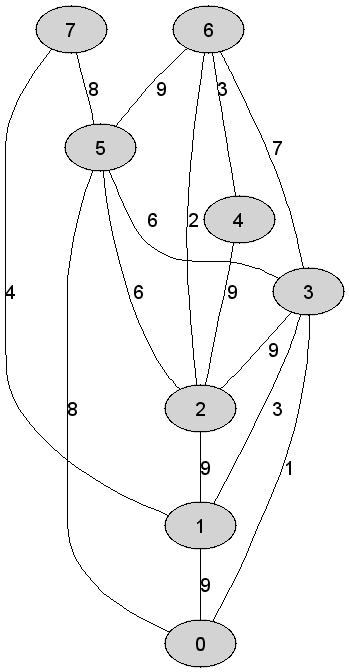
|
| Kolejność akceptowania krawędzi grafu do drzewa rozpinającego w trakcie wykonania rozważanego algorytmu jest następująca: 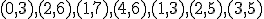 | 0 | | |
| Maksymalna waga krawędzi tworzącej otrzymane drzewo rozpinające grafu  jest równa co najmniej jest równa co najmniej 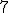 | 0 | | |
| Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem jego
finalnej postaci, jest równa dokładnie 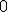 | 1 | + | |
| 12 | Rozważmy tablicę 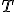 indeksowaną od indeksowaną od 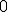 reprezentującą reprezentującą 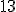 -elementowy częściowo uporządkowany ciąg liczb naturalnych: -elementowy częściowo uporządkowany ciąg liczb naturalnych: 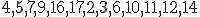 . Do całkowitego uporządkowania elementów owej tablicy stosujemy algorytm Merge. Które z poniższych zdań jest prawdziwe? . Do całkowitego uporządkowania elementów owej tablicy stosujemy algorytm Merge. Które z poniższych zdań jest prawdziwe? |
| Elementy tablicy 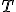 , które w algorytmie Merge są argumentami ostatniej operacji porównania elmentów, to kolejno , które w algorytmie Merge są argumentami ostatniej operacji porównania elmentów, to kolejno 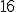 oraz oraz 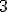 | 0 | | |
| Elementy tablicy 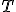 , które w algorytmie Merge są argumentami ostatniej operacji porównania elmentów, to kolejno , które w algorytmie Merge są argumentami ostatniej operacji porównania elmentów, to kolejno 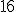 oraz oraz 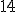 | 1 | + | |
| Elementy tablicy 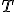 , które w algorytmie Merge nie są argumentami ostatniej operacji porównania elmentów, to kolejno , które w algorytmie Merge nie są argumentami ostatniej operacji porównania elmentów, to kolejno 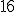 oraz oraz 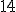 | 0 | | |
| 13 | Rozważmy nieskierowany graf prosty 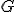 z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od 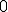 do do 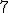 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 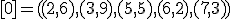 , , 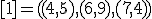 , , 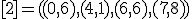 , , 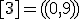 , , 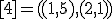 , , 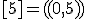 , , 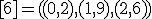 , , 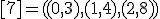 i przedstawiony na poniższym rysunku. Dla grafu i przedstawiony na poniższym rysunku. Dla grafu 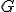 i wierzchołka startowego i wierzchołka startowego 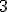 stosujemy stosujemy algorytm Prima wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru wierzchołków, jako
pierwszy wybieramy wierzchołek z mniejszą etykietą.
stosujemy stosujemy algorytm Prima wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru wierzchołków, jako
pierwszy wybieramy wierzchołek z mniejszą etykietą. 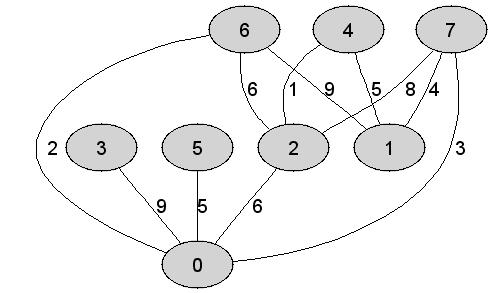
|
| Kolejność przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu 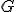 w trakcie wykonania algorytmu Prima jest następująca: w trakcie wykonania algorytmu Prima jest następująca: 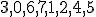 | 0 | | |
| Suma wag krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania algorytmu Prima jest równa dokładnie 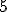 | 0 | | |
| Suma wag krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania algorytmu Prima jest równa dokładnie 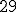 | 1 | + | |
| 14 | Rozważmy tablicę 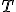 reprezentującą reprezentującą 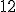 -elementowy ciąg -elementowy ciąg 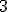 -cyfrowych liczb naturalnych: -cyfrowych liczb naturalnych: 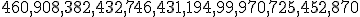 .
Do posortowania owej tablicy stosujemy algorytm RadixSort
zaimplementowany przy użyciu kolejek. Które z poniższych zdań jest
prawdziwe? .
Do posortowania owej tablicy stosujemy algorytm RadixSort
zaimplementowany przy użyciu kolejek. Które z poniższych zdań jest
prawdziwe? |
| Łączna liczba operacji IN we wszystkich kolejkach w trakcie wykonania rozważanego algorytmu jest równa dokładnie 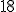 | 0 | | |
| Tuż po sortowaniu liczb względem cyfr na 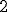 -ej pozycji dziesiętnej (liczonej od prawej do lewej strony), zawartość tablicy -ej pozycji dziesiętnej (liczonej od prawej do lewej strony), zawartość tablicy 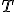 jest następująca: jest następująca: 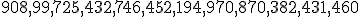 | 0 | | |
| Tuż po sortowaniu liczb względem cyfr na 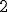 -ej pozycji dziesiętnej (liczonej od prawej do lewej strony), zawartość tablicy -ej pozycji dziesiętnej (liczonej od prawej do lewej strony), zawartość tablicy 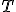 jest następująca: jest następująca: 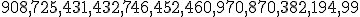 | 1 | + | |
| 15 | Rozważmy początkowo pustą strukturę stosu 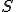 , do której wstawiono elementy: , do której wstawiono elementy: 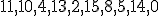 . Następnie na strukturze . Następnie na strukturze 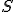 wykonano kolejno ciąg operacji: wykonano kolejno ciąg operacji: 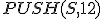 , , 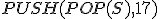 , , 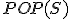 , , 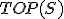 , , 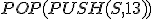 , , 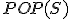 , , 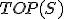 , , 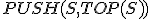 . Które z poniższych zdań jest prawdziwe? . Które z poniższych zdań jest prawdziwe? |
| Maksymalna wysokość stosu 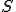 w trakcie wykonania przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: w trakcie wykonania przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: 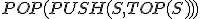 , , 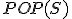 , , 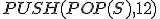 , , 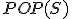 , , 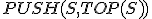 , , 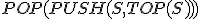 , , 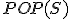 , , 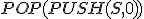 | 1 | + | |
| Ostateczna wysokość stosu 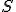 tuż po wykonaniu przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: tuż po wykonaniu przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: 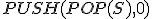 , , 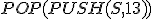 , , 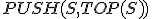 , , 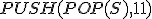 , , 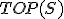 , , 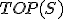 , , 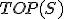 , , 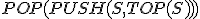 | 0 | | |
| Ostateczna wysokość stosu 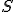 tuż po wykonaniu przedstawionego ciągu operacji jest równa dokładnie tuż po wykonaniu przedstawionego ciągu operacji jest równa dokładnie 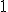 | 0 | | |
| 16 | Rozważmy algorytm 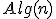 , gdzie , gdzie 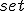 jest typem danych reprezentującym podzbiory zbioru jest typem danych reprezentującym podzbiory zbioru 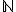 - set A:=
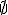 ; ; - int i:=0;
- while (i < n) do
- A:=A
 {i}; {i}; - i:=i+1;
- od
- return A;
Które z następujących zdań jest prawdziwe? |
| Jeżeli 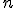 jest liczbą naturalną większą od zera, to po wykonaniu algorymu spełnione są warunki jest liczbą naturalną większą od zera, to po wykonaniu algorymu spełnione są warunki 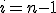 oraz oraz 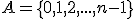 | 0 | | |
| Niezmiennikiem pętli w algorytmie 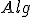 jest formuła jest formuła 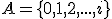 | 0 | | |
| Niezmiennikiem pętli w algorytmie 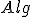 jest formuła jest formuła 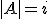 | 1 | + | |
| 17 | Koszt algorytmu Partition, zastosowanego do ciągu o 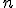 elementach jest: elementach jest: |
| 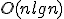 , jeżeli operacją dominującą jest porównanie elementów , jeżeli operacją dominującą jest porównanie elementów | 1 | + | |
| 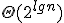 , jeżeli operacją dominującą jest porównanie elementów , jeżeli operacją dominującą jest porównanie elementów | 1 | + | |
| Rzędu 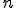 , jeżeli operacją dominującą jest przestawienie elementów , jeżeli operacją dominującą jest przestawienie elementów | 0 | | |
| 18 | Które z wymienionych zdań jest prawdziwe? |
| Długość dowolnej drogi od korzenia do liścia w drzewie decyzyjnym dla algorytmu sortowania przez wybór zastosowanego do ciągu 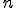 elementowego wynosi co najwyżej elementowego wynosi co najwyżej 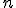 | 0 | | |
| Algorytm InsertionSort, zastosowany do ciągu uporządkowanego o 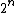 elementach, wykonuje tylko elementach, wykonuje tylko 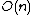 przestawień przestawień | 1 | + | |
| Algorytm InsertionSort wykonuje dla ciągu odwrotnie uporządkowanego asymptotycznie mniej porównań niż algorytm SelectionSort | 0 | | |
| 19 | Niech 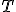 będzie drzewem BST powstałym przez kolejne wstawianie wierzchołków o etykietach będzie drzewem BST powstałym przez kolejne wstawianie wierzchołków o etykietach 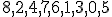 do początkowo pustej struktury. Które z ponizszych zdań jest prawdziwe? do początkowo pustej struktury. Które z ponizszych zdań jest prawdziwe? |
| Usunięcie wierzchołka z etykietą 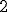 w drzewie w drzewie 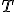 prowadzi do drzewa, w którym w miejscu wierzchołka z etykietą prowadzi do drzewa, w którym w miejscu wierzchołka z etykietą 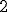 znajdzie się wierzchołek z etykietą znajdzie się wierzchołek z etykietą 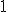 albo albo 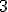 | 1 | + | |
| Usunięcie wierzchołka z etykietą 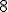 w drzewie w drzewie 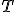 prowadzi do drzewa, którego korzeniem będzie wierzchołek z etykietą prowadzi do drzewa, którego korzeniem będzie wierzchołek z etykietą 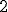 | 1 | + | |
| Wysokość drzewa 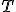 jest niezależna od kolejności wstawiania rozważanych wierzchołków jest niezależna od kolejności wstawiania rozważanych wierzchołków | 0 | | |
| 20 | Niech 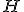 będzie kopcem-drzewem o będzie kopcem-drzewem o 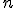 wierzchołkach i niech wierzchołkach i niech 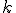 będzie liczbą jego liści na ostatnim poziomie. Zaznacz zdania prawdziwe. będzie liczbą jego liści na ostatnim poziomie. Zaznacz zdania prawdziwe. |
| Jeśli 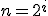 , dla pewnego , dla pewnego 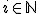 , to , to 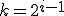 | 0 | | |
| Jeśli 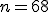 , to , to 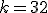 | 0 | | |
| Jeśli 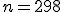 , to , to 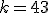 | 1 | + | |

