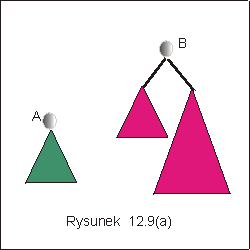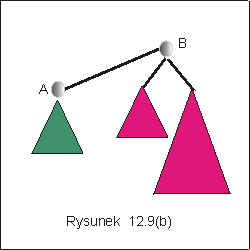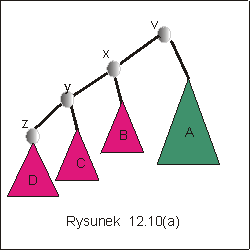Problem
Dana jest rodzina niepustych i rozłącznych zbiorów. Na zbiorach tej rodziny wykonywać będziemy dwie operacje:

Niech E będzie zbiorem elementów, P(E) zbiorem wszystkich podzbiorów zbioru E, oraz P niech będzie rodziną podzbiorów zbioru E, tzn. P należy do zbioru P(P(E)). Wtedy

przy czym, Find(P, x) = A wttw A Î P oraz x Î A
Union (P,A,B) = P' wttw A Ï P' oraz B Ï P' oraz (A + B) Î P(P(A)), dla dowolnych A, B Î P.

Naszym zadaniem w tym punkcie jest znalezienie adekwatnej struktury danych, pozwalającej stosować operacje Find i Union z możliwie niskim kosztem.

Istnieje wiele różnych implementacji tej struktury. Wiele z nich używa po prostu tablic do reprezentowania zbiorów i ich rodzin. Najlepszym jednak sposobem implementacji są drzewa. O tej właśnie implementacji będzie mowa w tym punkcie.

Przyjmijmy, że każdy zbiór A rozważanej rodziny P jest reprezentowany przez drzewo, którego węzły są etykietowane elementami zbioru A. Drzewo takie nie musi być birarne. Załóżmy, że w każdym węźle takiego drzewa zapamiętany jest element zbioru A, jako wartość atrybutu et, oraz referencja do pozycji zajmowanej przez ojca tego wierzchołka, zapisana jako wartość atrybutu father. Oczywiście korzeń drzewa nie ma ojca. Jego etykietę będziemy uznawali za nazwę zbioru, do którego należą etykiety zgromadzone w wierzchołkach tego drzewa. Zakładamy ponadto, że mając element zbioru X, mamy również dostęp do węzła drzewa o takiej właśnie etykiecie. Można to zrealizować numerując wszystkie etykiety liczbami naturalnymi i wpisując wierzchołek z i-tą etykietą do specjalnej tablicy na pozycję i-tą.

Przykład 5.1
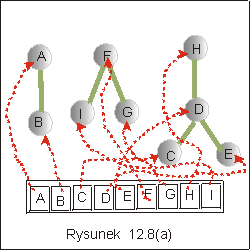
Rozważmy graf G którego podziały zbioru wierzchołków przedstawiliśmy na rysunku 12.7. Rodzina zbiorów {{A,B}, {F,I,G}, {C,D,E,H}}, będąca uzyskanym w szóstym kroku, podziałem zbioru wierzchołków grafu, może być reprezentowana przez zbiór drzew przedstawionych na rysunku 12.8(a). Zauważmy, że krawędzie w tym drzewie nie odpowiadają krawędziom grafu G: na przykład w grafie G nie ma krawędzi FG.

Operację Find można zrealizować następująco: aby znaleźć zbiór, do którego należy wskazany element, przechodzimy "w górę" drzewa zgodnie z referencją father. Gdy dojdziemy do korzenia, odczytujemy nazwę drzewa. Oczywiście dwa elementy należą do tego samego drzewa, jeśli idąc po dowiązaniach father, od węzłów przechowujących te elementy, dochodzimy do tego samego korzenia. Gdybyśmy chcieli zbadać do jakiego drzewa należy element C, to idąc po czerwonym dowiązaniu znajdziemy wierzchołek o etykiecie C, a potem posługując się zielonymi dowiązaniami przejdziemy do D i do H. Drzewo, które zawiera element C, jest więc wskazane przez etykietę H.

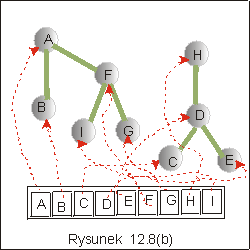
Wykonanie operacji Union polega na połączeniu dwóch drzew. Możemy to zrealizować przez dowiązanie korzenia jednego drzewa do korzenia drugiego drzewa. Na rysunku 12.8(b) przedstawiono wynik wykonania operacji Union dla drzew o korzeniach w A i w F: do korzenia drzewa A dowiązaliśmy korzeń drzewa F. Wszystkie elementy A, B, F, G, I należą teraz do drzewa o korzeniu A.

Koszt operacji Union jest stały, nie zależy od liczby elementów przechowywanych w łączonych drzewach. Natomiast koszt operacji Find zależy od wysokości drzewa, które przeglądamy. W najgorszym przypadku, gdy drzewo składa się z jednej ścieżki, koszt tej operacji mógłby być liniowy ze względu na liczbę elementów zbioru X. Jeśli mamy uzyskać mniejszy koszt tej operacji musimy się postarać by wysokość drzew nie rosła zbyt szybko. Zauważmy, że wysokość drzewa rośnie tylko w wyniku operacji Union: wszystkie węzły jednego z drzew przesuwają się o jeden poziom w dół. Dla tych węzłów ścieżka będzie dłuższa. Naturalną metodą łagodzącą ten efekt jest tzw. balansowanie lub wyważanie. Balansowanie polega na dowiązywaniu drzewa o mniejszej wysokości do korzenia drzewa o większej wysokości. Taką modyfikację operacji Union możemy wykonać z kosztem stałym, jeśli w korzeniu każdego z drzew rodziny, będziemy pamiętali dodatkowo wysokość drzewa. Na rysunku 12.9(b) przedstawiono wynik zastosowania opeacji Union z balansowaniem do drzew A i B z rysunku 12.(a). Ponieważ drzewo B jest wyższe, to do jego korzenia dowiązujemy drzewo A.

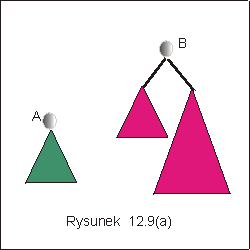
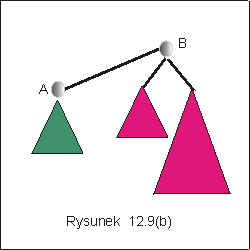
Drugą metodą zmniejszania wysokości drzew reprezentujących rodzinę zbiorów rozłącznych jest tzw. kompresja ścieżek. Kompresja ścieżek polega na tym, że w trakcie wykonywania operacji Find, wszystkie napotkane na ścieżce do korzenia wierzchołki, dowiązujemy bezpośrednio do korzenia. Wymaga to dwukrotnego pokonania ścieżki od węzła początkowego do korzenia. Najpierw szukamy nazwy drzewa, do którego należy etykieta. Następnie, mając referencję do korzenia tego drzewa, możemy przejść ponownie po tej samej ścieżce i zmienić wszystkie dowiązania tak, by wskazywały bezpośrednio korzeń drzewa. Wprawdzie wykonaliśmy więcej operacji, ale następne wykonania operacji Find, o ile będą dotyczyły wierzchołków z tej ścieżki, będą mogły być wykonane w jednym kroku.
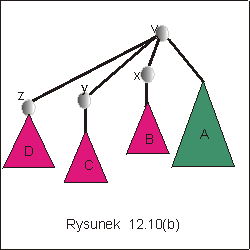
Na rysunku 12.10(a) przedstawiono przykładowe drzewo pewnego podziału. Efekt wykonania operacji Find dla wierzchołka z został przedstawiony na rysunku 12.10(b). Wierzchołki x,y,z sš teraz synami wierzchołka v. Dzięki temu koszt następnego wyszukiwania tych wierzchołków będzie stały, a koszt wyszukiwania wierzchołków znajdujących się w drzewach B, C i D zmniejszy się.

Następujący lemat wskazuje jak skuteczne jest takie postępowanie:

Wniosek
Koszt algorytmu Kruskala, w implementacji struktury Find-Union na drzewach z balansowaniem i kompresją ścieżek, wynosi O(m lg n), gdzie m jest liczbą krawędzi, a n liczbą wierzchołków grafu.
Rzeczywiście, koszt utworzenia kolejki priorytetowej zawierającej wszystkie krawędzie grafu wynosi O(m lg m), lub biorą pod uwagę wierzchołki grafu O(m lg n). W pętli powtarzamy dwukrotnie wykonanie operacji Find i raz operacji Union. Łącznie daje to ciąg długości co najwyżej O(m) operacji Find i Union. Na mocy Lematu 5.1 łączny koszt wykonania pętli jest prawie liniowy, co ostatecznie daje oszacowanie kosztu algorytmu Kruskala na O(m lg n).

Pytanie 7: Rozważmy graf 12.2 i zastosujmy do niego algorytm Kruskala zaimplementowany na drzewach z balansowaniem i kompresją ścieżek. Jaka jest wysokość drzewa w ostanim podziale zbioru wierzchołków grafu?