| Nr | Opcja | Punkty | Poprawna | Odpowiedź |
|---|
| 1 | Rozważmy nieskierowany graf prosty 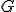 , którego wierzchołki etykietowane są liczbami naturalnymi od , którego wierzchołki etykietowane są liczbami naturalnymi od 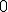 do do 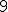 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 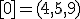 , , 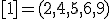 , , 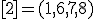 , , 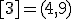 , , 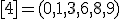 , , 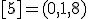 , , 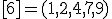 , , 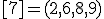 , , 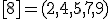 , , 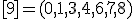 i przedstawiony na poniższym rysunku. Dla grafu i przedstawiony na poniższym rysunku. Dla grafu 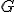 stosujemy algorytm kolorowania LF (largest first). Które z poniższych
zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości
wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą
etykietą. Kolory indeksujemy od
stosujemy algorytm kolorowania LF (largest first). Które z poniższych
zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości
wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą
etykietą. Kolory indeksujemy od 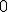 . . 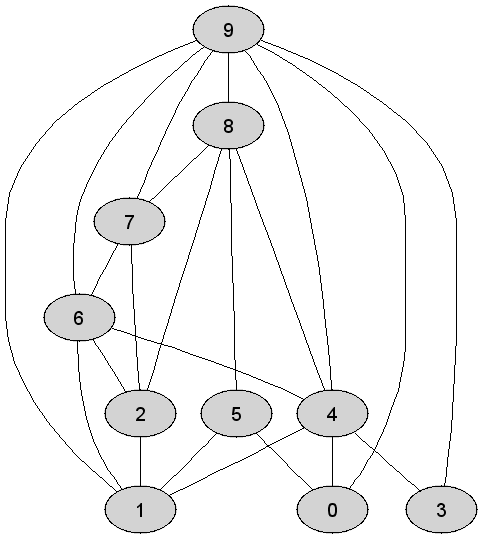
|
| Kolejność kolorowania wierzchołków grafu 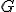 w trakcie wykonania algorytmu LF jest następująca: w trakcie wykonania algorytmu LF jest następująca: 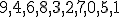 | 0 | | |
| Po zastosowaniu algorytm LF wierzchołek 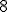 ma przypisany taki sam kolor jak wierzchołek ma przypisany taki sam kolor jak wierzchołek 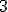 | 1 | + | |
| Kolejność kolorowania wierzchołków grafu 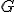 w trakcie wykonania algorytmu LF jest następująca: w trakcie wykonania algorytmu LF jest następująca: 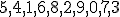 | 0 | | |
| 2 | Rozważmy kopiec binarny 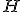 typu min zaimplementowany w drzewie binarnym i powstały na skutek kolejnego wstawiania elementów ciągu typu min zaimplementowany w drzewie binarnym i powstały na skutek kolejnego wstawiania elementów ciągu 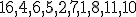 do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe? do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe? |
| Jeżeli zamiast drzewa binarnego do implementacji kopca binarnego  użyjemy tablicy, to jej finalna postać będzie następująca: użyjemy tablicy, to jej finalna postać będzie następująca: 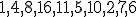 | 0 | | |
| Etykiety wierzchołków drzewa-kopca  wypisane w kolejności PostOrder tworzą ciąg: wypisane w kolejności PostOrder tworzą ciąg: 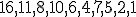 | 0 | | |
| Etykiety wierzchołków drzewa-kopca 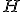 wypisane w kolejności PostOrder tworzą ciąg: wypisane w kolejności PostOrder tworzą ciąg: 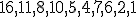 | 1 | + | |
| 3 | Rozważmy kopiec binarny 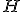 typu min zaimplementowany w drzewie binarnym. Kopiec typu min zaimplementowany w drzewie binarnym. Kopiec 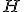 konstruujemy z elementów ciągu konstruujemy z elementów ciągu 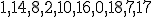 stosując szybki algorytm budowy kopca HeapConstruct. Które z poniższych zdań jest prawdziwe? stosując szybki algorytm budowy kopca HeapConstruct. Które z poniższych zdań jest prawdziwe? |
| Liczba wierzchołków wewnętrznych drzewa-kopca 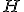 jest równa dokładnie jest równa dokładnie 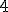 | 0 | | |
| Etykiety wierzchołków drzewa-kopca 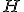 wypisane w kolejności InOrder tworzą ciąg: wypisane w kolejności InOrder tworzą ciąg: 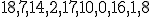 | 1 | + | |
| Jeżeli zamiast drzewa binarnego do implementacji kopca binarnego 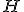 użyjemy tablicy, to jej finalna postać będzie następująca: użyjemy tablicy, to jej finalna postać będzie następująca: 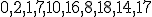 | 1 | + | |
| 4 | Rozważmy kopiec binarny 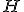 typu min zaimplementowany w drzewie binarnym. Kopiec typu min zaimplementowany w drzewie binarnym. Kopiec 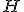 konstruujemy z elementów ciągu konstruujemy z elementów ciągu 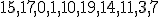 stosując szybki algorytm budowy kopca HeapConstruct. Następnie w kopcu stosując szybki algorytm budowy kopca HeapConstruct. Następnie w kopcu 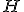 wykonujem wykonujem 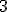 -krotnie operaję DELMIN. Które z poniższych zdań jest prawdziwe? -krotnie operaję DELMIN. Które z poniższych zdań jest prawdziwe? |
| Liczba wierzchołków wewnętrznych drzewa-kopca 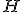 jest równa dokładnie jest równa dokładnie 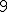 | 0 | | |
| Wysokość drzewa-kopca 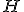 jest równa dokładnie jest równa dokładnie 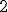 | 1 | + | |
| Etykiety wierzchołków drzewa-kopca 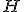 wypisane w kolejności InOrder tworzą ciąg: wypisane w kolejności InOrder tworzą ciąg: 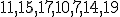 | 0 | | |
| 5 | Rozważmy drzewo kodowe Huffmana 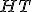 powstałe na skutek zastosowania algorytmu budowy drzewa kodu Huffmana
dla ciągu znaków zawierającego odpowiednio (znak - krotność wystąpień):
powstałe na skutek zastosowania algorytmu budowy drzewa kodu Huffmana
dla ciągu znaków zawierającego odpowiednio (znak - krotność wystąpień):
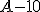 , , 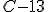 , , 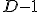 , , 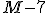 , , 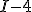 , , 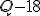 , , 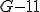 , , 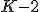 .
Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku
niejednoznacznego wyboru poddrzew, za mniejsze uznajemy to, którego
etykiet liści czytane od lewej do prawej strony tworzą słowo mniejsze w
sensie porządku leksykograficznego. .
Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku
niejednoznacznego wyboru poddrzew, za mniejsze uznajemy to, którego
etykiet liści czytane od lewej do prawej strony tworzą słowo mniejsze w
sensie porządku leksykograficznego. |
| Kod litery 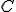 odczytany z drzewa odczytany z drzewa 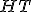 jest następujący: jest następujący: 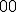 | 1 | + | |
| Kod litery 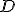 odczytany z drzewa odczytany z drzewa 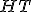 jest następujący: jest następujący: 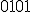 | 0 | | |
| Kod litery 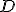 odczytany z drzewa odczytany z drzewa 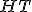 jest następujący: jest następujący: 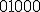 | 1 | + | |
| 6 | Rozważmy nieskierowany graf prosty 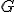 z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od 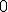 do do 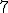 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 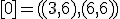 , , 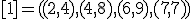 , , 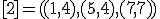 , , 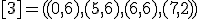 , , 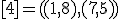 , , 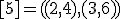 , , 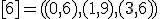 , , 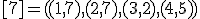 i przedstawiony na poniższym rysunku. Dla grafu i przedstawiony na poniższym rysunku. Dla grafu 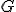 i wierzchołka startowego i wierzchołka startowego 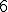 stosujemy stosujemy algorytm Prima wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru wierzchołków, jako
pierwszy wybieramy wierzchołek z mniejszą etykietą.
stosujemy stosujemy algorytm Prima wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru wierzchołków, jako
pierwszy wybieramy wierzchołek z mniejszą etykietą. 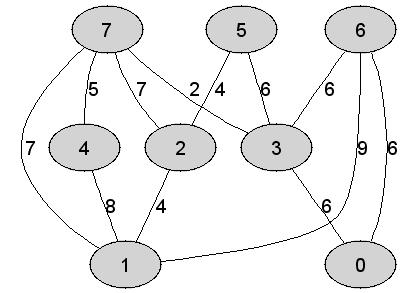
|
| Kolejność przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu 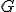 w trakcie wykonania algorytmu Prima jest następująca: w trakcie wykonania algorytmu Prima jest następująca: 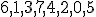 | 0 | | |
| Wysokość minimalego drzewa rozpinającego będącego rezultatem działania algorytmu Prima jest równa dokładnie 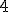 | 1 | + | |
| Liczba
wierzchołków zewnętrznych w minimalym drzewie rozpinającym będącym
rezultatem działania algorytmu Prima jest równa dokładnie 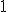 | 0 | | |
| 7 | Rozważmy zachłanny algorytm PrimTSP rozwiązujący problem komiwojażera w 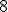 -wierzchołkowym grafie -wierzchołkowym grafie 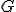 , którego wierzchołki etykietowane są liczbami naturalnymi od , którego wierzchołki etykietowane są liczbami naturalnymi od 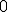 do do 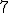 włącznie i rozmieszczone są w odpowiednio następujących punktach płaszczyzny euklidesowej: włącznie i rozmieszczone są w odpowiednio następujących punktach płaszczyzny euklidesowej: 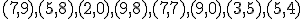 . Które z poniższych zdań jest prawdziwe jeżeli wierzchołkiem startowym jest . Które z poniższych zdań jest prawdziwe jeżeli wierzchołkiem startowym jest 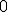 ? Uwaga! W przypadku niejednoznacznej możliwości wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą etykietą. ? Uwaga! W przypadku niejednoznacznej możliwości wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą etykietą. |
| Krawędź 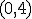 należy do wyznaczonego cyklu Hamiltona w grafie należy do wyznaczonego cyklu Hamiltona w grafie 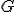 | 1 | + | |
| Kolejność przyłączania wierzchołków do konstruowanego cyklu Hamiltona w trakcie wykonania algorytmu PrimTSP jest następująca: 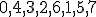 | 0 | | |
| Maksymalna wysokość stosu pomocniczego użytego do realizacji przejścia grafu 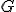 metodą DFS w celu wyznaczenia cyklu Hamiltona jest równa dokładnie metodą DFS w celu wyznaczenia cyklu Hamiltona jest równa dokładnie 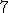 | 0 | | |
| 8 | Jaka
będzie kolejność elementów tablicy po wykonaniu algorytmu
Construct, konstrukcji kopca w tablicy, jeśli na początku tablica
zawierała liczby 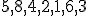 (w podanym porządku)? (w podanym porządku)? |
| Kolejność elementów nie ulegnie zmianie | 0 | | |
| Taka sama jak w przypadku tablicy postaci początkowej 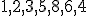 | 1 | + | |
| 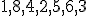 | 0 | | |
| 9 | Co robi następujący algorytm 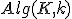 , gdzie , gdzie 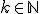 - int i;
- for i:=1 to k do
- K:=delmin(K);
- od;
- return min(K);
jeśli 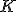 jest kopcem o jest kopcem o 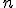 elementach i elementach i 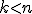 ? ? |
| Znajduje 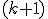 -szy co do wielkosci element kopca -szy co do wielkosci element kopca 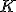 | 1 | + | |
| Znajduje 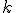 -ty co do wielkości element kopca -ty co do wielkości element kopca 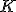 | 0 | | |
| Z kosztem 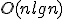 ze względu na liczbę operacji porównań elementów kopca ze względu na liczbę operacji porównań elementów kopca 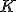 , znajduje , znajduje 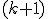 -szy największy element struktury -szy największy element struktury | 1 | + | |
| 10 | Rozważmy tekst składający się z symboli będących cyframi dziesiętnymi ze zbioru 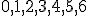 , gdzie cyfra , gdzie cyfra 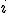 występuje: występuje: 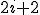 razy, jeżeli razy, jeżeli 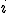 jest liczbą parzystą, jest liczbą parzystą,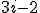 razy, jeżeli razy, jeżeli 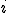 jest liczbą nieparzystą. jest liczbą nieparzystą.
Na
podstawie rozważanego tekstu zbudowano drzewo kodowe Huffmana. Który z
poniższych kodów binarnych reprezentuje zadaną liczbę naturalną 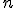 ? ? |
| 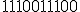 , jeżeli , jeżeli 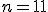 | 1 | + | |
| 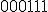 , jeżeli , jeżeli 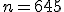 | 0 | | |
| 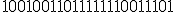 , jeżeli , jeżeli 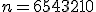 | 1 | + | |
| 11 | Rozważmy nieskierowany graf prosty 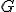 z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od 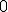 do do 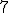 włącznie, zadany tabicą list sąsiedztwa postaci: włącznie, zadany tabicą list sąsiedztwa postaci: 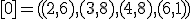 , , 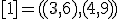 , , 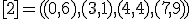 , , 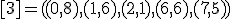 , , 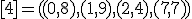 , , 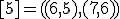 , , 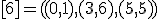 , , 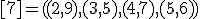 i przedstawiony na poniższym rysunku. Dla grafu i przedstawiony na poniższym rysunku. Dla grafu  stosujemy algorytm Kruskala wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru krawędzi, jako pierwszą
wybieramy krawędź, której etykiety wierzchołków krańcowych w kolejności
niemalejącej tworzą mniejszą liczbę naturalną.
stosujemy algorytm Kruskala wyznaczenia minimalnego drzewa
rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W
przypadku niejednoznacznej możliwości wyboru krawędzi, jako pierwszą
wybieramy krawędź, której etykiety wierzchołków krańcowych w kolejności
niemalejącej tworzą mniejszą liczbę naturalną. 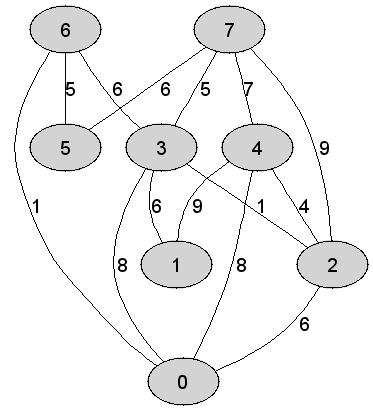
|
| Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego
finalnej postaci, jest równa dokładnie 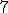 | 1 | + | |
| Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego
finalnej postaci, jest równa dokładnie 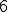 | 0 | | |
| Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem jego
finalnej postaci, jest równa dokładnie 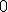 | 1 | + | |
| 12 | Rozważmy zachłanny algorytm KruskalTSP rozwiązujący problem komiwojażera w 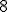 -wierzchołkowym grafie -wierzchołkowym grafie 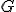 , którego wierzchołki etykietowane są liczbami naturalnymi od , którego wierzchołki etykietowane są liczbami naturalnymi od 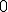 do do 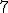 włącznie i rozmieszczone są w odpowiednio następujących punktach płaszczyzny euklidesowej: włącznie i rozmieszczone są w odpowiednio następujących punktach płaszczyzny euklidesowej: 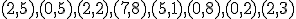 .
Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku
niejednoznacznej możliwości wyboru krawędzi, jako pierwszą wybieramy
krawędź, której etykiety wierzchołków krańcowych w kolejności
niemalejącej tworzą mniejszą liczbę naturalną. .
Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku
niejednoznacznej możliwości wyboru krawędzi, jako pierwszą wybieramy
krawędź, której etykiety wierzchołków krańcowych w kolejności
niemalejącej tworzą mniejszą liczbę naturalną. |
| Kolejność
akceptowania krawędzi grafu do konstruowanego cyklu Hamiltona w trakcie
wykonania rozważanego algorytmu jest następująca: 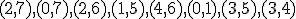 | 0 | | |
| Kolejność
akceptowania krawędzi grafu do konstruowanego cyklu Hamiltona w trakcie
wykonania rozważanego algorytmu jest następująca: 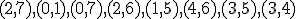 | 1 | + | |
| Krawędź 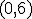 należy do wyznaczonego cyklu Hamiltona w grafie należy do wyznaczonego cyklu Hamiltona w grafie 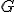 | 0 | | |

